Inferring physical parameters¶
This tutorial describes how to infer physical parameters from the free parameters of a phenomenological model for the scintillation velocities of a pulsar on a circular orbit whose radiation is scattered by a single one-dimensional screen. The tutorial builds upon a preceding tutorial in which such a phenomenological model is fit to a time series of scintillation velocities.
For a derivation of the equations seen here, refer to the scintillation velocities background. Further explanations can be found in Marten’s scintillometry page and Daniel Baker’s “Orbital Parameters and Distances” document. As in that document, the practical example here uses the parameter values for the pulsar PSR J0437–4715 as derived by Reardon et al. (2020).
The combined codeblocks in this tutorial can be downloaded as a Python script and as a Jupyter notebook:
- Python script:
- Jupyter notebook:
Preliminaries¶
Imports.
import numpy as np
import matplotlib.pyplot as plt
from astropy import units as u
from astropy import constants as const
from astropy.coordinates import SkyCoord
from astropy.visualization import quantity_support
Set up support for plotting Astropy’s
Quantity objects, and make sure that the
output of plotting commands is displayed inline (i.e., directly below the code
cell that produced it).
quantity_support()
%matplotlib inline
Set known parameters¶
Set the pulsar system’s coordinates \((\alpha_\mathrm{p}, \delta_\mathrm{p})\) and proper motion components \((\mu_\mathrm{p,sys,\alpha\ast}, \mu_\mathrm{p,sys,\delta})\), as well as some of the system’s parameters that are known from timing studies: its orbital period \(P_\mathrm{orb,p}\), projected semi-major axis \(a_\mathrm{p} \sin( i_\mathrm{p} )\), and radial-velocity amplitude \(K_\mathrm{p} = 2 \pi a_\mathrm{p} \sin( i_\mathrm{p} ) / P_\mathrm{orb,p}\) [which relates to the pulsar’s mean orbital speed as \(v_\mathrm{0,p} = K_\mathrm{p} / \sin( i_\mathrm{p} )\)].
psr_coord = SkyCoord('04h37m15.99744s -47d15m09.7170s',
pm_ra_cosdec=121.4385 * u.mas / u.yr,
pm_dec=-71.4754 * u.mas / u.yr)
p_orb_p = 5.7410459 * u.day
asini_p = 3.3667144 * const.c * u.s
k_p = 2.*np.pi * asini_p / p_orb_p
Set the known properties of Earth’s orbit (the orbital period \(P_\oplus\), its semi-major axis \(a_\oplus\), and the mean orbital speed \(v_{0,\oplus} = 2 \pi a_\oplus / P_\mathrm{orb,\oplus}\)), and derive its orientation with respect to the line of sight (i.e., the orbit’s inclination \(i_\oplus\) and longitude of ascending node \(\Omega_\oplus\)).
p_orb_e = 1. * u.yr
a_e = 1. * u.au
v_0_e = 2.*np.pi * a_e / p_orb_e
psr_coord_eclip = psr_coord.barycentricmeanecliptic
ascnod_eclip = SkyCoord(lon=psr_coord_eclip.lon - 90.*u.deg, lat=0.*u.deg,
frame='barycentricmeanecliptic')
ascnod_equat = ascnod_eclip.icrs
i_e = psr_coord_eclip.lat + 90.*u.deg
omega_e = psr_coord.position_angle(ascnod_equat)
Warning
This calculation assumes that Earth’s orbit is circular, which is of course not completely accurate. As noted above, the pulsar’s orbit is also assumed to be circular. These simplifications result in a model in which it is clear how the scintillation velocities depend on the physical parameters of the system, but this model can clearly be improved by implementing more realistic orbits for the pulsar and Earth.
The model parameters¶
The phenomenological model used to fit the scaled effective velocities \(\left| v_\mathrm{eff,\parallel} \right| / \sqrt{d_\mathrm{eff}}\) consists of two sinusoids (with known periods) and an offset:
Here, \(\phi_\oplus\) and \(\phi_\mathrm{p}\) are the orbital phases of the Earth and the pulsar, respectively, measured from their ascending nodes. The free parameters in this equation are the amplitudes of Earth’s and the pulsar’s orbital scaled-effective-velocity modulation \(A_\oplus\) and \(A_\mathrm{p}\) (assumed to be non-negative: \(A_\oplus \geq 0\), \(A_\mathrm{p} \geq 0\)), their phase offsets \(\chi_\oplus\) and \(\chi_\mathrm{p}\), and a constant scaled-effective-velocity offset \(C\).
We want to figure out how these model parameters are related to the system’s physical parameters of interest, which are: the pulsar’s orbital inclination \(i_\mathrm{p}\), the pulsar’s longitude of ascending node \(\Omega_\mathrm{p}\), the distance to the pulsar \(d_\mathrm{p}\), the distance to the screen \(d_\mathrm{s}\), the position angle of the lens \(\xi\), and the velocity of the lens \(v_\mathrm{lens,\parallel}\) (in this tutorial, velocities with subscript \(\parallel\) refer to the component of the full three-dimensional velocity that is along the line of images formed by the lens). In terms of these physical parameters, the model parameters can be expressed as
where \(\arctantwo(y, x)\) refers to the 2-argument arctangent function. These equations contain several auxiliary parameters that need to be defined. As usual, \(d_\mathrm{eff}\) refers to the effective distance and \(s\) is the fractional screen–pulsar distance (with \(0 < s < 1\)). They are related to the distances of the pulsar and the screen according to
The factors \(b_\oplus\) and \(b_\mathrm{p}\), which modify the sinusoid amplitudes (with \(0 \leq b \leq 1\)), are given by (omitting the subscripts)
The symbols \(\Delta\Omega_\oplus\) and \(\Delta\Omega_\mathrm{p}\) denote the angles from the position angle of the screen to the longitude of ascending node of the orbit of the pulsar and the Earth, respectively, i.e.,
Finally, \(v_\mathrm{p,sys,\parallel}\) is the pulsar’s systemic velocity projected onto the line of images formed by the lens. It is given by
where \(\mu_\mathrm{p,sys}\) denotes the pulsar system’s proper motion projected onto the line of images.
For the example in this tutorial, we use the values for the model parameters found in the preceding tutorial.
amp_e = 1.91 * u.km/u.s/u.pc**0.5
amp_p = 1.34 * u.km/u.s/u.pc**0.5
chi_e = (65.14 * u.deg + [0., 180.] * u.deg) % (360.*u.deg)
chi_p = (245.83 * u.deg + [0., 180.] * u.deg) % (360.*u.deg)
dveff_c = 14.67 * u.km/u.s/u.pc**0.5 * [1., -1.]
Because of the modulus operation in the model equation, there are two possible solutions for the model parameters \((A_\oplus, A_\mathrm{p}, \chi_\oplus, \chi_\mathrm{p}, C)\). These differ from each other in the sign of \(C\) and a \(180^\circ\) rotation of the phase offsets \(\chi_\oplus\) and \(\chi_\mathrm{p}\). The amplitudes \(A_\oplus\) and \(A_\mathrm{p}\) remain the same in both solutions. As we will see, the two solution are equivalent except for a \(180^\circ\) difference in the orientation of the scattering screen on the sky. We can use either set of values to find the same constraints on physical parameters.
Note
In the example (based on the real parameters of pulsar PSR J0437–4715), the difference between the phase offsets \(\chi_\oplus\) and \(\chi_\mathrm{p}\) is also close to \(180^\circ\). This is merely a coincidence and has no physical relevance.
Constraints without additional information¶
Let’s first consider the general case in which none of the six physical parameters of interest \((i_\mathrm{p}, \Omega_\mathrm{p}, d_\mathrm{p}, d_\mathrm{s}, \xi, v_\mathrm{lens,\parallel})\) are known. Since the fit only provides five constraints, not all six physical parameters will have a unique solution. Nevertheless, it is possible to constrain some of the parameters, and derive relations between the remaining ones.
The position angle of the screen¶
The first physical parameter to infer from the free parameters of our model is the position angle of the screen \(\xi\). This parameter can be computed from the fitted phase offset of Earth’s orbital velocity signature \(\chi_\oplus\) and the known orientation of Earth’s orbit (\(i_\oplus\) and \(\Omega_\oplus\)), using the equation
delta_omega_e = np.arctan2(np.sin(chi_e) / np.cos(i_e), np.cos(chi_e))
xi = (delta_omega_e + omega_e) % (360.*u.deg)
print(f'xi: {xi[0].to(u.deg):.2f} or {xi[1].to(u.deg):.2f}')
xi: 314.87 deg or 134.87 deg
The two solutions for \(\xi\) correspond to rotating the screen by \(180^\circ\) on the sky. This ambiguity in screen orientation cannot be resolved using single-telescope data, but it does not make a difference in the values found for the remaining parameters (except for the sign of the lens velocity \(v_\mathrm{lens,\parallel}\)). By convention, the angle \(\xi\) is restricted to the range \(0^\circ \leq \xi < 180^\circ\) (i.e., we use the convention that \(\xi\) refers to the position angle of the eastern half of the line of lensed images). To make some of the upcoming computations a bit more straightforward, we now pick the \(\xi\) solution that adheres to this convention, and continue using only the values of \(\chi_\oplus\), \(\chi_\mathrm{p}\), and \(C\) that correspond to this solution.
j_sol = np.argwhere(xi < 180.*u.deg)[0,0]
print(f'xi: {xi[j_sol].to(u.deg):8.2f}')
print(f'chi_e: {chi_e[j_sol].to(u.deg):8.2f}')
print(f'chi_p: {chi_p[j_sol].to(u.deg):8.2f}')
print(f'dveff_c: {dveff_c[j_sol].to(u.km/u.s/u.pc**0.5):8.2f}')
xi: 134.87 deg
chi_e: 245.14 deg
chi_p: 65.83 deg
dveff_c: -14.67 km / (pc(1/2) s)
You can verify that the two solution are equivalent by setting j_sol to the
index of the other solution. Executing the codeblocks below should then give
the same answers for the physical parameters.
The orientation of the pulsar’s orbit¶
Knowing \(\xi\), it is possible to retrieve a relation between \(i_\mathrm{p}\) and \(\Omega_\mathrm{p}\) from the equation
i_p = np.linspace(0.*u.deg, 180.*u.deg, 181)
delta_omega_p = np.arctan2(np.sin(chi_p[j_sol]) / np.cos(i_p),
np.cos(chi_p[j_sol]))
omega_p = (xi[j_sol] - delta_omega_p) % (360.*u.deg)
The \(i_\mathrm{p}\)–\(\Omega_\mathrm{p}\) relation we found is disjointed at \(i_\mathrm{p} = 90^\circ\), where \(\cos( i_\mathrm{p} )\) changes sign. To avoid a line at the discontinuity, we plot the two halves separately.
plt.figure(figsize=(7., 6.))
ii_ccw = (i_p <= 90.*u.deg)
ii_cw = (i_p > 90.*u.deg)
plt.plot(i_p[ii_ccw].to(u.deg), omega_p[ii_ccw].to(u.deg),
label=r"pulsar's longitude of ascending node $\Omega_\mathrm{p}$")
plt.plot(i_p[ii_cw].to(u.deg), omega_p[ii_cw].to(u.deg), c='C0')
plt.plot([0., 180.] * u.deg, [1., 1.] * omega_e.to(u.deg), c='C1',
label=r"Earth's longitude of ascending node $\Omega_{\!\oplus}$")
plt.plot([0., 180.] * u.deg, [1., 1.] * xi[j_sol].to(u.deg), '--', c='gray',
label=r"position angle of line of lensed images $\xi$")
plt.xlim(0., 180.)
plt.ylim(0., 360.)
plt.xticks(np.linspace(0., 180., 7))
plt.yticks(np.linspace(0., 360., 9))
plt.legend()
plt.xlabel(r"pulsar's orbital inclination $i_\mathrm{p}$")
plt.ylabel('angle on the sky (east of north)')
plt.show()
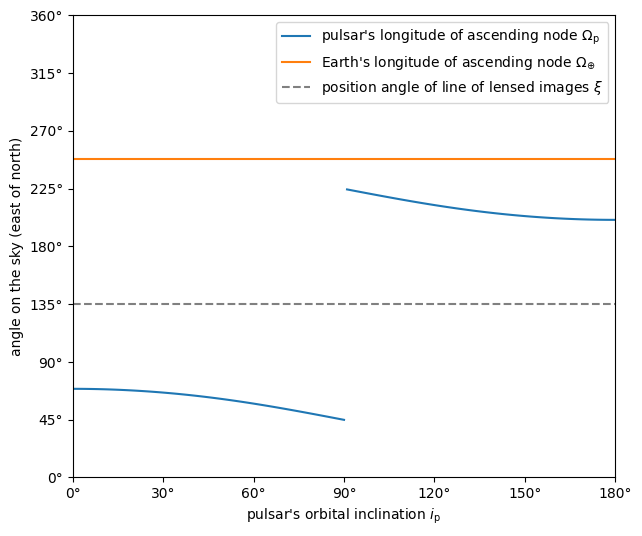
Plotting the relations shows how \(\Omega_\mathrm{p}\) is restricted to two ranges of values (while \(i_\mathrm{p}\) is still unrestricted).
print(f'{omega_p[ii_ccw][-1].to(u.deg):.2f} < omega_p < '
f'{omega_p[ii_ccw][ 0].to(u.deg):.2f} or '
f'{omega_p[ii_cw][ -1].to(u.deg):.2f} < omega_p < '
f'{omega_p[ii_cw][ 0].to(u.deg):.2f}')
44.87 deg < omega_p < 69.04 deg or 200.70 deg < omega_p < 224.42 deg
The effective distance¶
Next, the effective distance \(d_\mathrm{eff}\) can be calculated using
b2_e = (1. - np.sin(i_e)**2) / (1. - np.sin(i_e)**2 * np.cos(chi_e[j_sol])**2)
d_eff = v_0_e**2 / amp_e**2 * b2_e
print(f'd_eff: {d_eff.to(u.pc):8.2f}')
d_eff: 214.05 pc
Given the effective distance, it is possible to derive a relation between the distance to the pulsar \(d_\mathrm{p}\) and the distance to the screen \(d_\mathrm{s}\) in terms of the fractional screen–pulsar distance \(s\) (with \(0 < s < 1\)):
ns = 250
s = np.linspace(0.5/ns, 1. - 0.5/ns, ns)
d_s = s * d_eff
d_p = d_s / (1. - s)
plt.figure(figsize=(7., 6.))
plt.plot([0., 1.], [1., 1.] * d_eff.to(u.pc), '--', c='gray',
label=r'effective distance $d_\mathrm{eff}$')
plt.plot(s, d_p.to(u.pc), label=r'pulsar distance $d_\mathrm{p}$')
plt.plot(s, d_s.to(u.pc), label=r'screen distance $d_\mathrm{s}$')
plt.yscale('log')
plt.xlim(0., 1.)
plt.ylim(10., 1.e4)
plt.legend(loc='upper left')
plt.xlabel(r'fractional screen-pulsar distance $s$')
plt.ylabel(r'distance from Earth (pc)')
plt.show()
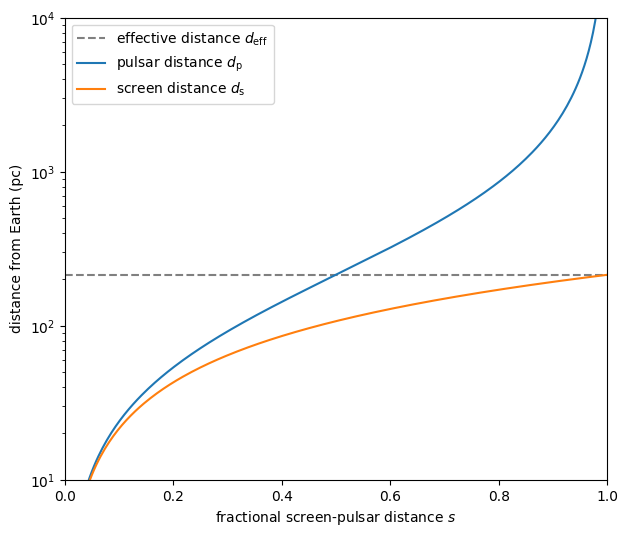
This also shows that the effective distance sets a maximum on the distance to the screen \(d_\mathrm{s} < d_\mathrm{eff}\).
Pulsar distance–orbital inclination relation¶
The aplitude of the pulsar’s orbital velocity signature \(A_\mathrm{p}\) can be used to derive a relation between the distance to the pulsar system \(d_\mathrm{p}\) and the sine of its orbital inclination \(\sin( i_\mathrm{p} )\), following
nsini_p = 250
sini_p = np.linspace(0.5/nsini_p, 1. - 0.5/nsini_p, nsini_p)
b2_p = (1. - sini_p**2) / (1. - sini_p**2 * np.cos(chi_p[j_sol])**2)
d_p = v_0_e * k_p / (amp_e * amp_p) * np.sqrt(b2_e * b2_p) / sini_p
plt.figure(figsize=(7., 6.))
plt.plot(sini_p, d_p.to(u.pc))
plt.yscale('log')
plt.xlim(0., 1.)
plt.ylim(10., 1.e4)
plt.xlabel(r"sine of pulsar's orbital inclination $\sin( i_\mathrm{p} )$")
plt.ylabel(r"pulsar's distance from Earth $d_\mathrm{p}$ (pc)")
plt.show()
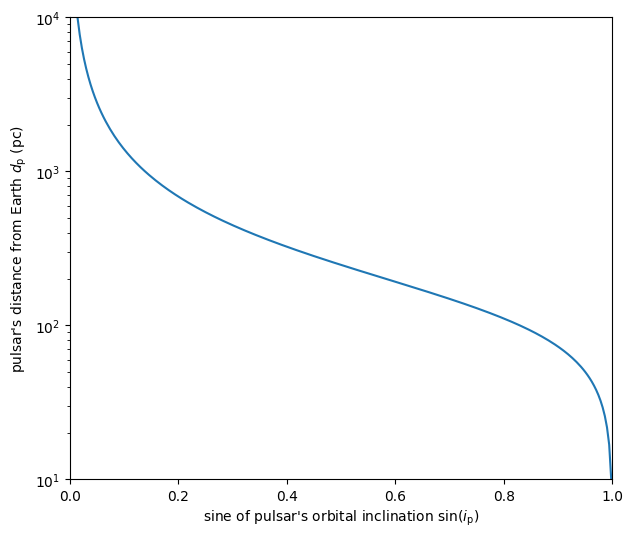
The lens velocity¶
Finally, it is possible to find a constraint on the projected lens velocity \(v_\mathrm{lens,\parallel}\). This is best expressed in terms of some intermediate quantities derived above (\(\xi\) and \(d_\mathrm{eff}\)) and as a function the fractional screen–pulsar distance \(s\):
where \(v_\mathrm{eff,\parallel,p,sys}\) denotes the contribution of the pulsar’s systemic motion to the effective velocity \(v_\mathrm{eff,\parallel}\):
To compute a velocity from a proper motion and a distance, we use the
dimensionless_angles() equivalency. This
takes care of handling the units of Astropy Quantity
objects correctly when using the small-angle approximation
(for further explanation, see the Astropy documentation about equivalencies).
s = [[0.], [1.]]
mu_p_sys = psr_coord.pm_ra_cosdec * np.sin(xi) + psr_coord.pm_dec * np.cos(xi)
v_eff_p_sys = (d_eff * mu_p_sys
).to(u.km/u.s, equivalencies=u.dimensionless_angles())
v_lens = s * (v_eff_p_sys + np.sqrt(d_eff) * dveff_c)
plt.figure(figsize=(7., 6.))
plt.plot(s, v_lens.to(u.km/u.s))
plt.xlim(0., 1.)
plt.legend([f'$\\xi = {xi_i.to_value(u.deg):.0f}^\\circ$' for xi_i in xi])
plt.xlabel(r'fractional screen-pulsar distance $s$')
plt.ylabel(r'lens velocity $v_\mathrm{lens,\!\parallel}$ (km/s)')
plt.show()
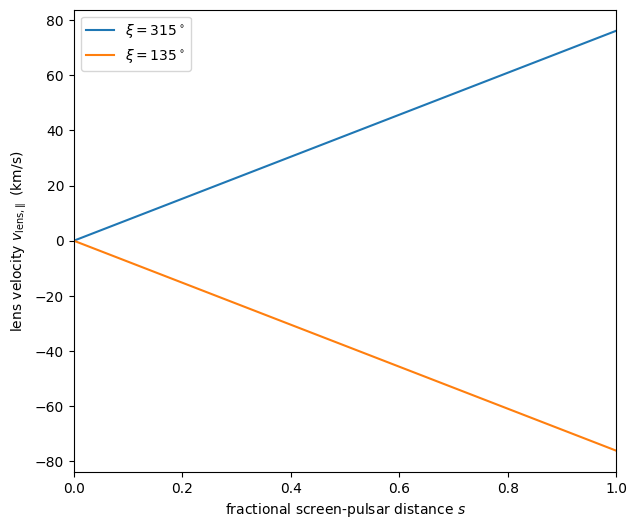
Note that these two solutions represent the same velocity on the sky: the sign flip is cancelled by the \(180^\circ\) rotation in direction.
Constraints with a known pulsar distance¶
We now consider situations in which there is additional information that provides constraints on one of the six physical parameters of interest. Together with the five constraints from scintillometry, this will allow better constraints on the remaining physical parameters of interest, although some ambiguity will remain.
In many cases, some external constraints exist on the distance to the pulsar. An example of such an constraint would be a parallax measurement. While in reality there will always be some uncertainty associated with the constraint, here we will assume perfect knowledge to examine how this constrains the remaining parameters. Another tutorial considers how statistical uncertainties in the distance and model parameters can be propagated to the physical parameters.
Set the known pulsar distance \(d_\mathrm{p}\).
d_p = 156.79 * u.pc
The screen distance¶
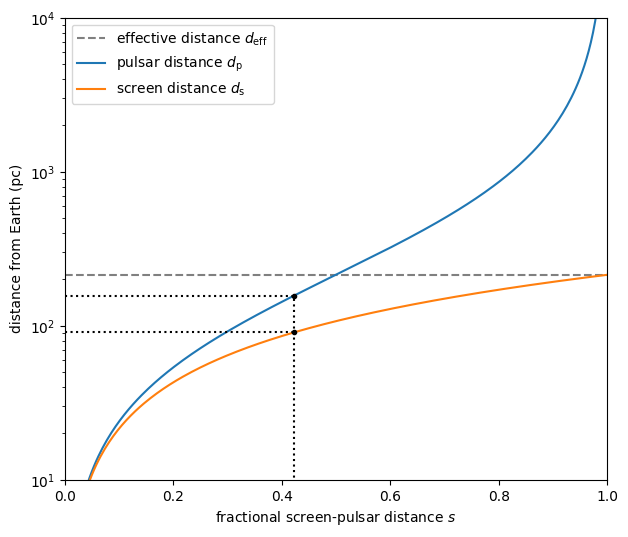
First of all, together with the scintillometric constraint on the effective distance \(d_\mathrm{eff}\), this immediately sets the distance to the screen \(d_\mathrm{s}\) and the fractional screen–pulsar distance \(s\).
d_s = d_p * d_eff / (d_p + d_eff)
s = 1. - d_s / d_p
print(f'd_s: {d_s.to(u.pc):8.2f}')
print(f's: {s:8.2f}')
d_s: 90.50 pc
s: 0.42
ns = 250
s_all = np.linspace(0.5/ns, 1. - 0.5/ns, ns)
d_s_all = s_all * d_eff
d_p_all = d_s_all / (1. - s_all)
plt.figure(figsize=(7., 6.))
plt.plot([0., 1.], [1., 1.] * d_eff.to(u.pc), '--', c='gray',
label=r'effective distance $d_\mathrm{eff}$')
plt.plot(s_all, d_p_all.to(u.pc), label=r'pulsar distance $d_\mathrm{p}$')
plt.plot(s_all, d_s_all.to(u.pc), label=r'screen distance $d_\mathrm{s}$')
plt.plot(s, d_p.to(u.pc), 'k.')
plt.plot([0., 1., 1.] * s, [1., 1., 1.e-30] * d_p.to(u.pc), ':k')
plt.plot(s, d_s.to(u.pc), 'k.')
plt.plot([0., 1.] * s, [1., 1.] * d_s.to(u.pc), ':k')
plt.yscale('log')
plt.xlim(0., 1.)
plt.ylim(10., 1.e4)
plt.legend(loc='upper left')
plt.xlabel(r'fractional screen-pulsar distance $s$')
plt.ylabel(r'distance from Earth (pc)')
plt.show()
Pulsar orbital inclination¶
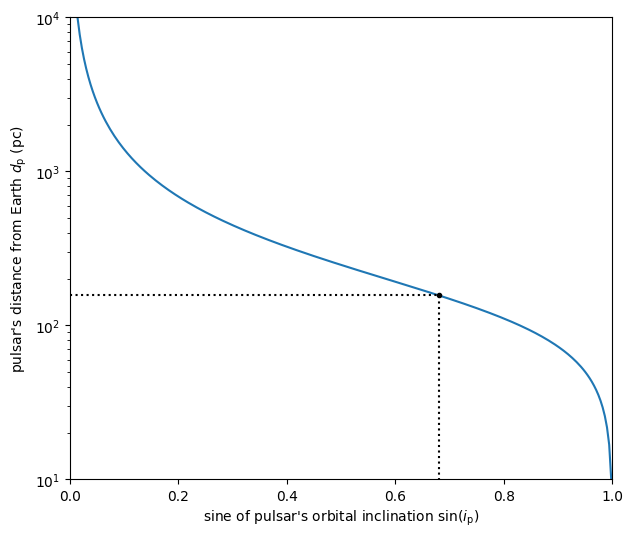
Next, the relation between pulsar distance and orbital inclination can be solved for \(\sin( i_\mathrm{p} )\). This relation first needs to be rewritten as a quadratic equation in \(\sin^2( i_\mathrm{p} )\):
We then compute the solutions of the quadratic equation using Muller’s version of the quadratic formula [which has the advantage over the standard quadratic formula of also giving a valid root for \(\cos^2( \chi_\mathrm{p} ) = 0\)]:
Of these two solutions, only the one with the plus sign lies in the range \(0 \le \sin^2( i_\mathrm{p} ) \le 1\) for all valid combinations of \(\chi_\mathrm{p}\) and \(Z\), yielding a single solution for \(\sin( i_\mathrm{p} )\) that corresponds to two possible values of \(i_\mathrm{p}\), symmetric around \(90^\circ\).
z2 = b2_e * (v_0_e * k_p / (amp_e * amp_p * d_p))**2
cos2chi_p = np.cos(chi_p[j_sol])**2
discrim = (1. + z2)**2 - 4. * cos2chi_p * z2
sin2i_p = 2. * z2 / (1. + z2 + np.sqrt(discrim))
sini_p = np.sqrt(sin2i_p).to(u.dimensionless_unscaled)
i_p = [1., -1.] * np.arcsin(sini_p) % (180.*u.deg)
print(f'sin(i_p): {sini_p:8.2f}')
print(f'\ni_p: {i_p[0].to(u.deg):.2f} or {i_p[1].to(u.deg):.2f}')
sin(i_p): 0.68
i_p: 42.83 deg or 137.17 deg
nsini_p = 250
sini_p_all = np.linspace(0.5/nsini_p, 1. - 0.5/nsini_p, nsini_p)
b2_p = (1. - sini_p_all**2) / (1. - sini_p_all**2 * np.cos(chi_p[j_sol])**2)
d_p_all = v_0_e * k_p / (amp_e * amp_p) * np.sqrt(b2_e * b2_p) / sini_p_all
plt.figure(figsize=(7., 6.))
plt.plot(sini_p_all, d_p_all.to(u.pc))
plt.plot(sini_p, d_p.to(u.pc), 'k.')
plt.plot([0., 1., 1.] * sini_p, [1., 1., 1.e-30] * d_p.to(u.pc), ':k')
plt.yscale('log')
plt.xlim(0., 1.)
plt.ylim(10., 1.e4)
plt.xlabel(r"sine of pulsar's orbital inclination $\sin( i_\mathrm{p} )$")
plt.ylabel(r"pulsar's distance from Earth $d_\mathrm{p}$ (pc)")
plt.show()
Pulsar’s longitude of ascending node¶
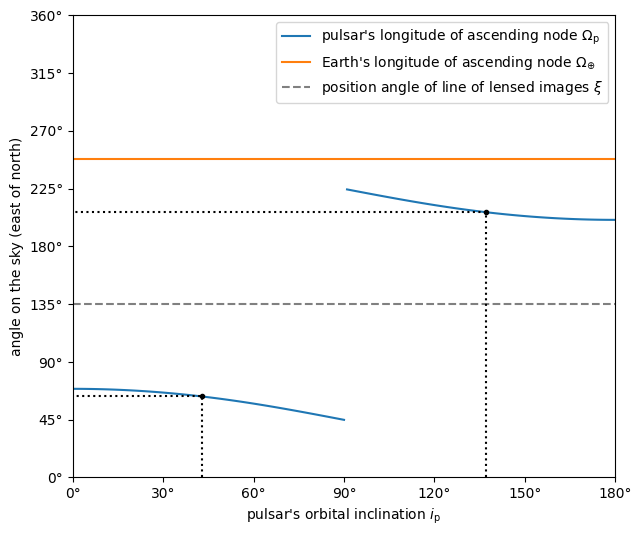
Knowing \(\sin( i_\mathrm{p} )\), it is possible to constrain the pulsar’s longitude of ascending node to two possible values.
cosi_p = [1., -1.] * np.sqrt(1. - sin2i_p)
delta_omega_p = np.arctan2(np.sin(chi_p[j_sol]) / cosi_p, np.cos(chi_p[j_sol]))
omega_p = (xi[j_sol] - delta_omega_p) % (360.*u.deg)
for k in [0, 1]:
print(f'omega_p: {omega_p[k].to(u.deg):8.2f} for '
f'i_p: {i_p[k].to(u.deg):8.2f}')
omega_p: 63.09 deg for i_p: 42.83 deg
omega_p: 206.65 deg for i_p: 137.17 deg
i_p_all = np.linspace(0.*u.deg, 180.*u.deg, 181)
delta_omega_p_all = np.arctan2(np.sin(chi_p[j_sol]) / np.cos(i_p_all),
np.cos(chi_p[j_sol]))
omega_p_all = (xi[j_sol] - delta_omega_p_all) % (360.*u.deg)
plt.figure(figsize=(7., 6.))
ii_ccw = (i_p_all <= 90.*u.deg)
ii_cw = (i_p_all > 90.*u.deg)
plt.plot(i_p_all[ii_ccw].to(u.deg), omega_p_all[ii_ccw].to(u.deg),
label=r"pulsar's longitude of ascending node $\Omega_\mathrm{p}$")
plt.plot(i_p_all[ii_cw].to(u.deg), omega_p_all[ii_cw].to(u.deg), c='C0')
plt.plot([0., 180.] * u.deg, [1., 1.] * omega_e.to(u.deg), c='C1',
label=r"Earth's longitude of ascending node $\Omega_{\!\oplus}$")
plt.plot([0., 180.] * u.deg, [1., 1.] * xi[j_sol].to(u.deg), '--', c='gray',
label=r"position angle of line of lensed images $\xi$")
plt.plot(i_p.to(u.deg), omega_p.to(u.deg), 'k.')
for k in [0, 1]:
plt.plot([1., 1., 0.] * i_p[k].to(u.deg),
[0., 1., 1.] * omega_p[k].to(u.deg), ':k')
plt.xlim(0., 180.)
plt.ylim(0., 360.)
plt.xticks(np.linspace(0., 180., 7))
plt.yticks(np.linspace(0., 360., 9))
plt.legend()
plt.xlabel(r"pulsar's orbital inclination $i_\mathrm{p}$")
plt.ylabel('angle on the sky (east of north)')
plt.show()
The lens velocity¶
Finally, with \(s\) known, only one possible lens velocity remains.
v_lens = s * (v_eff_p_sys + np.sqrt(d_eff) * dveff_c)
for j in [0, 1]:
print(f'v_lens: {v_lens[j].to(u.km/u.s):8.2f} for '
f'xi: {xi[j].to(u.deg):8.2f}')
v_lens: 32.19 km / s for xi: 314.87 deg
v_lens: -32.19 km / s for xi: 134.87 deg
s_all = [[0.], [1.]]
v_lens_all = s_all * (v_eff_p_sys + np.sqrt(d_eff) * dveff_c)
plt.figure(figsize=(7., 6.))
plt.plot(s_all, v_lens_all.to(u.km/u.s))
ylims = plt.gca().get_ylim()
plt.plot([1., 1.] * s, v_lens.to(u.km/u.s), 'k.')
plt.plot([0., 1., 1.] * s, [1., 1., -10.] * v_lens[0].to(u.km/u.s), ':k')
plt.plot([0., 1.] * s, [1., 1.] * v_lens[1].to(u.km/u.s), ':k')
plt.xlim(0., 1.)
plt.ylim(ylims)
plt.legend([f'$\\xi = {xi_i.to_value(u.deg):.0f}^\\circ$' for xi_i in xi])
plt.xlabel(r'fractional screen-pulsar distance $s$')
plt.ylabel(r'lens velocity $v_\mathrm{lens,\!\parallel}$ (km/s)')
plt.show()
