Fitting scintillation velocities¶
This tutorial describes how to fit a phenomenological model to a time series of
scintillation velocities for a pulsar in a circular orbit and a single
one-dimensional screen. It builds upon a preceding tutorial that explains how such a time series can be artificially
generated. A pre-made time series (with artificial noise) is available for
download: fake-data-J0437.npz
For a derivation of the equations seen here, refer to the scintillation velocities background. Further explanations can be found in Marten’s scintillometry page and Daniel Baker’s “Orbital Parameters and Distances” document. As in that document, the practical example here uses the parameter values for the pulsar PSR J0437–4715 as derived by Reardon et al. (2020).
The combined codeblocks in this tutorial can be downloaded as a Python script and as a Jupyter notebook:
- Python script:
- Jupyter notebook:
Preliminaries¶
Imports.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import CenteredNorm
# Note: matplotlib.colors.CenteredNorm requires matplotlib version >= 3.4.0
from astropy import units as u
from astropy.time import Time
from astropy.coordinates import SkyCoord
from astropy.visualization import quantity_support, time_support
from scipy.optimize import curve_fit
Set up support for plotting Astropy’s
Quantity and Time
objects, and make sure that the output of plotting commands is displayed inline
(i.e., directly below the code cell that produced it).
quantity_support()
time_support(format='iso')
%matplotlib inline
Define some line and marker properties to easily give the model and the data a consistent appearance throughout the notebook. Also assign two rather long label strings to variables, so they don’t need to be rewritten for each plot, and define a little dictionary of arguments to move plot titles inside their axes.
obs_style = {
'linestyle': 'none',
'color': 'grey',
'marker': 'o',
'markerfacecolor': 'none'
}
mdl_style = {
'linestyle': '-',
'linewidth': 2,
'color': 'C0'
}
dveff_lbl = (r'scaled effective velocity '
r'$\dfrac{ | v_\mathrm{eff,\!\!\parallel} | }'
r'{ \sqrt{ d_\mathrm{eff} } }$ '
r'$\left( \dfrac{ \mathrm{km/s} }'
r'{ \sqrt{ \mathrm{pc} } } \right)$')
dveff_signed_lbl = (r'scaled effective velocity '
r'$\dfrac{ v_\mathrm{eff,\!\!\parallel} }'
r'{ \sqrt{ d_\mathrm{eff} } }$ '
r'$\left( \dfrac{ \mathrm{km/s} }'
r'{ \sqrt{ \mathrm{pc} } } \right)$')
title_kwargs = {
'loc': 'left',
'x': 0.01,
'y': 1.0,
'pad': -14
}
Set known parameters¶
Set the pulsar’s orbital period \(P_\mathrm{orb,p}\) and time of ascending node \(t_\mathrm{asc,p}\), which are known from pulsar timing.
p_orb_p = 5.7410459 * u.day
t_asc_p = Time(54501.4671, format='mjd', scale='tdb')
Set the Earth’s orbital period \(P_\mathrm{orb,\oplus}\) and derive its time of ascending node \(t_\mathrm{asc,\oplus}\) from the pulsar’s coordinates.
p_orb_e = 1. * u.yr
t_eqx = Time('2005-03-21 12:33', format='iso', scale='utc')
psr_coord = SkyCoord('04h37m15.99744s -47d15m09.7170s')
psr_coord_eclip = psr_coord.barycentricmeanecliptic
t_asc_e = t_eqx + (psr_coord_eclip.lon + 90.*u.deg).to_value(u.cycle) * p_orb_e
Warning
This calculation assumes that Earth’s orbit is circular, which is of course not completely accurate. As noted above, the pulsar’s orbit is also assumed to be circular. These simplifications result in a model in which it is clear how the scintillation velocities depend on the physical parameters of the system, but this model can clearly be improved by implementing more realistic orbits for the pulsar and Earth.
Load and inspect the data¶
Load the data (available for download here:
fake-data-J0437.npz)
and convert the NumPy arrays that are stored in the file to Astropy
Time and Quantity
objects.
data = np.load('./data/fake-data-J0437.npz')
t_obs = Time(data['t_mjd'], format='mjd', scale='utc')
dveff_obs = data['dveff_obs'] * u.km/u.s/u.pc**0.5
dveff_err = data['dveff_err'] * u.km/u.s/u.pc**0.5
We can now precompute the orbital phases (measured from the ascending node) of Earth, \(\phi_\oplus(t)\), and the pulsar, \(\phi_\mathrm{p}(t)\), for the observation times:
ph_e_obs = ((t_obs - t_asc_e) / p_orb_e).to(u.dimensionless_unscaled) * u.cycle
ph_p_obs = ((t_obs - t_asc_p) / p_orb_p).to(u.dimensionless_unscaled) * u.cycle
Let’s have a look at all the data.
plt.figure(figsize=(11., 6.))
plt.errorbar(t_obs.jyear, dveff_obs, yerr=dveff_err, **obs_style, alpha=0.3)
plt.xlim(t_obs[0].jyear, t_obs[-1].jyear)
plt.xlabel('time')
plt.ylabel(dveff_lbl)
plt.show()
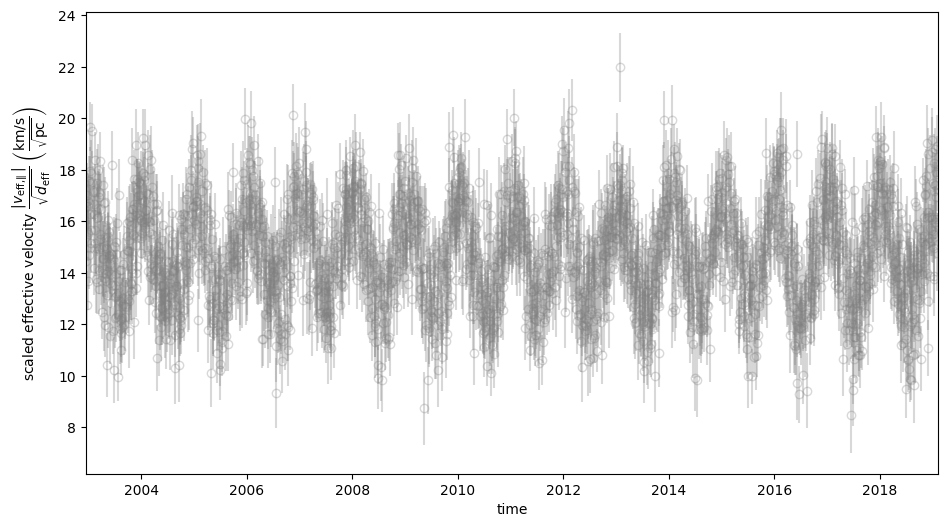
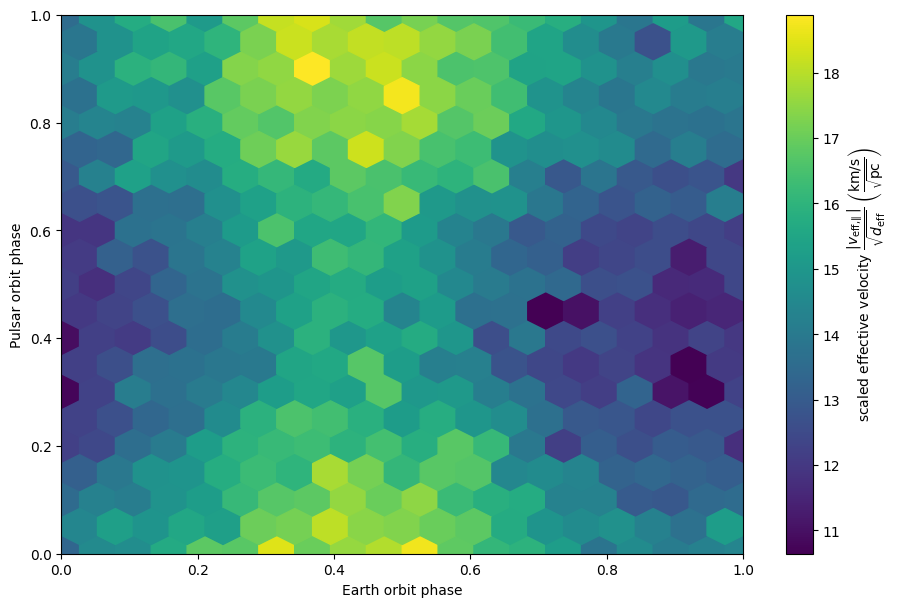
Because the pulsar’s orbital period is much shorter than the baseline of the observation, it cannot be discerned in the raw time series. To visualize the modulations in scintillation velocity caused by the pulsar’s orbital motion and that of the Earth in one plot, one should make a 2D phase fold of the dataset.
plt.figure(figsize=(11., 7.))
plt.hexbin(ph_e_obs.value % 1., ph_p_obs.value % 1., C=dveff_obs.value,
reduce_C_function=np.median, gridsize=19)
plt.xlim(0., 1.)
plt.ylim(0., 1.)
plt.xlabel('Earth orbit phase')
plt.ylabel('Pulsar orbit phase')
cbar = plt.colorbar()
cbar.set_label(dveff_lbl)
Note
For data sets in which the effective velocity flips sign (generally because the source has a low projected proper motion), the above plots will look qualitatively different.
The phenomenological model¶
There are many possible ways of writing the formula for scaled effective velocity, all with their advantages and disadvantages. Here, we model the velocities as the sum of two sinusoids with known periods (one for the pulsar’s orbital modulation and one for the Earth’s) and a constant offset (due to the pulsar’s systemic velocity and the motion of the lens). We then need to take the absolute value of this sum, because measuring the curvature of a parabola in a secondary spectrum only constrains the square of the effective velocity. Thus, the model is given by
There are five free parameters: the amplitudes of Earth’s and the pulsar’s orbital scaled-effective-velocity modulation, \(A_\oplus\) and \(A_\mathrm{p}\), their phase offsets, \(\chi_\oplus\) and \(\chi_\mathrm{p}\), and a constant scaled-effective-velocity offset, \(C\). The amplitudes should be non-negative (\(A_\oplus \geq 0\), \(A_\mathrm{p} \geq 0\)).
Because of the modulus operation in the model equation, there are two possible solutions for the model parameters \((A_\oplus, A_\mathrm{p}, \chi_\oplus, \chi_\mathrm{p}, C)\). These differ from each other in the sign of \(C\) and a \(180^\circ\) rotation of the phase offsets \(\chi_\oplus\) and \(\chi_\mathrm{p}\). The amplitudes \(A_\oplus\) and \(A_\mathrm{p}\) remain the same in both solutions. As we will see, the two solution are equivalent except for a \(180^\circ\) difference in the orientation of the scattering screen on the sky. We can use either set of values to find the same constraints on physical parameters.
This formulation of the scaled-effective-velocity equation has the advantage that it is clear how its free parameters affect the model in data space (hence, when fitting the model to data, it is clear how the fit can be improved by changing the the values of the free parameters). However, it obscures how the model depends on the physical parameters of interest. A follow-up tutorial describes how the free parameters in this equation are related to the physical parameters of the system.
When putting the model equation into a Python function, it is useful to keep the modulus operation separate from the rest of the model. This will allow us to model the individual components of the scaled effective velocity separately.
def model_dveff_signed(pars, t):
ph_e = ((t - t_asc_e) / p_orb_e).to(u.dimensionless_unscaled) * u.cycle
ph_p = ((t - t_asc_p) / p_orb_p).to(u.dimensionless_unscaled) * u.cycle
dveff_e = pars['amp_e'] * np.sin(ph_e - pars['chi_e'])
dveff_p = pars['amp_p'] * np.sin(ph_p - pars['chi_p'])
dveff = dveff_e + dveff_p + pars['dveff_c']
return (dveff).to(u.km/u.s/u.pc**0.5)
def model_dveff_abs(pars, t):
dveff_signed = model_dveff_signed(pars, t)
return np.abs(dveff_signed)
Note that the first argument of these functions, pars, should be a
dictionary containing the free parameters as
Quantity objects; their second argument,
t, should be a Time object containing the times
at which the model should be evaluated.
Estimating the free-parameter values by eye¶
When fitting a model to data, it is helpful to understand the effect of varying the different free parameters. One can, for example, start by evaluating the model at some random point in free-parameter space and then explore the space by varying the parameters one by one. In this case, however, the relation between the free parameters and the model is fairly clear from the model equation. Moreover, the (synthetic) data are of sufficient quality that we can make rough estimates of the free-parameters values simply by looking at the data.
The amplitudes \(A_\oplus\) and \(A_\mathrm{p}\) and the offset \(C\) can be estimated by eye from the time-series plot above:
\(A_\oplus\) is the amplitude of the sinusoid visible in the time-series (around 2 km/s/pc1/2);
\(A_\mathrm{p}\) is roughly the half-width of the band of data points that constitutes the visible sinusoid (around 1.5 km/s/pc1/2);
\(C\) corresponds to the mean of the time series or its negative (around ±15 km/s/pc1/2).
The phase offsets \(\chi_\oplus\) and \(\chi_\mathrm{p}\) are a bit harder to estimate by eye, but they can be inferred from the 2D phase fold of the dataset. For the positive-\(C\) solution, hypothetical phase-offsets of \((\chi_\oplus, \chi_\mathrm{p}) = (0^\circ, 0^\circ)\) would give a peak in the 2D sinusoid at phases \((0.25, 0.25)\). Since the peak in the plot seems to be around \((0.4, 0.9)\), we can estimate the phase offsets for the positive-\(C\) solution to be roughly \((\chi_\oplus, \chi_\mathrm{p}) \approx (0.15, 0.65) = (54^\circ, 234^\circ)\). For the other solution, the phase offsets should be \(180^\circ\) away from these values, i.e., \((\chi_\oplus, \chi_\mathrm{p}) \approx (234^\circ, 54^\circ)\) for \(C \approx -15\;\mathrm{km/s/pc^{1/2}}\).
To prepare a set of parameter values for use with our model functions, put them in a dictionary with the appropriate keys. Here we enter the positive-\(C\) solution:
pars_try = {
'amp_e': 2. * u.km/u.s/u.pc**0.5,
'amp_p': 1.5 * u.km/u.s/u.pc**0.5,
'chi_e': 54. * u.deg,
'chi_p': 234. * u.deg,
'dveff_c': 15. * u.km/u.s/u.pc**0.5
}
Note
In this example (based on the real parameters of pulsar PSR J0437–4715), the difference between the phase offsets \(\chi_\oplus\) and \(\chi_\mathrm{p}\) happens to be close to \(180^\circ\). This is merely a coincidence and has no physical relevance.
Visual model-data comparison¶
To test if a set of parameter values yields a good fit to the data, we should produce a few key model-data comparison figures. Since we will likely want to repeat these tests for different instances of the model, we will put them in Python functions that evaluate the model for a given set of parameter values and generate the desired plots. The resulting functions are somewhat lengthy; to avoid them interrupting the flow of the tutorial, they are by default hidden from view. The codeblocks with these functions can be expanded using the “Show function definition” buttons.
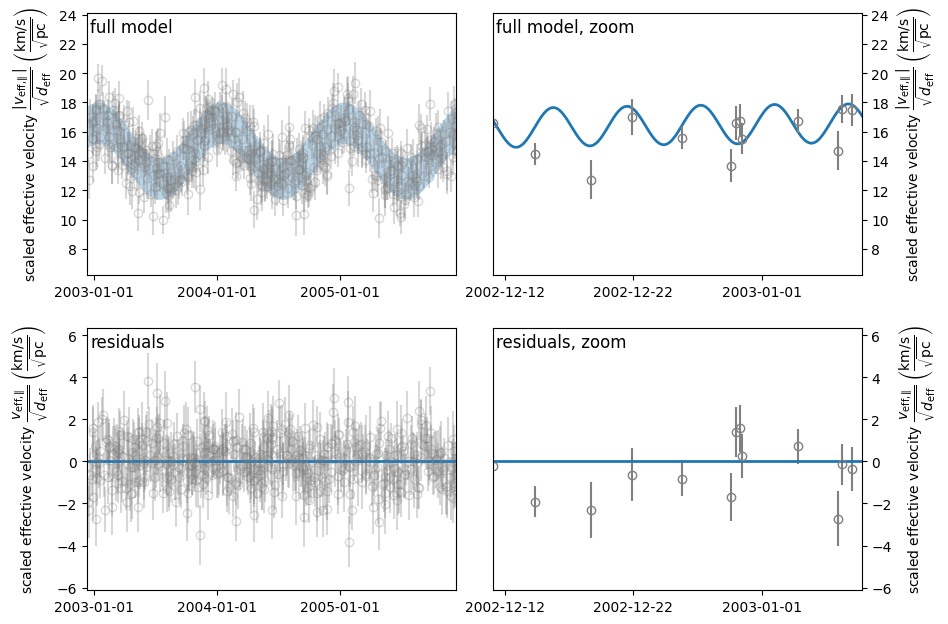
The most straightforward way of model-data comparison is to overplot the model on the data and show the residuals. Since the two orbital periods in the system under investigation have very different timescales, we show two different zooms of the time series: one in which the Earth’s orbital modulation is visible and one in which the pulsar’s can be resolved. The observations are relatively sparse compared to the pulsar’s orbital period, so to make the pulsar’s orbit visible in the time series, we have to also evaluate the model at a higher time resolution.
function definition
def visualize_model_full(pars):
dveff_mdl = model_dveff_abs(pars, t_obs)
dveff_res = dveff_obs - dveff_mdl
tlim_long = [t_obs[0].mjd, t_obs[0].mjd + 3. * p_orb_e.to_value(u.day)]
tlim_zoom = [t_obs[0].mjd, t_obs[0].mjd + 5. * p_orb_p.to_value(u.day)]
t_mjd_many = np.arange(tlim_long[0], tlim_long[-1], 0.2)
t_many = Time(t_mjd_many, format='mjd')
dveff_mdl_many = model_dveff_abs(pars, t_many)
plt.figure(figsize=(10., 7.5))
plt.subplots_adjust(wspace=0.1)
ax1 = plt.subplot(221)
plt.plot(t_many, dveff_mdl_many, **mdl_style, alpha=0.3)
plt.errorbar(t_obs.mjd, dveff_obs, yerr=dveff_err, **obs_style, alpha=0.3)
plt.xlim(tlim_long)
plt.title('full model', **title_kwargs)
plt.xlabel('')
plt.ylabel(dveff_lbl)
ax2 = plt.subplot(223, sharex=ax1)
plt.errorbar(t_obs.mjd, dveff_res, yerr=dveff_err, **obs_style, alpha=0.3)
plt.axhline(**mdl_style)
plt.xlim(tlim_long)
plt.title('residuals', **title_kwargs)
plt.ylabel(dveff_signed_lbl)
ax3 = plt.subplot(222, sharey=ax1)
plt.plot(t_many, dveff_mdl_many, **mdl_style)
plt.errorbar(t_obs.mjd, dveff_obs, yerr=dveff_err, **obs_style)
plt.xlim(tlim_zoom)
plt.title('full model, zoom', **title_kwargs)
plt.xlabel('')
plt.ylabel(dveff_lbl)
ax3.yaxis.set_label_position('right')
ax3.yaxis.tick_right()
ax4 = plt.subplot(224, sharex=ax3, sharey=ax2)
plt.errorbar(t_obs.mjd, dveff_res, yerr=dveff_err, **obs_style)
plt.axhline(**mdl_style)
plt.xlim(tlim_zoom)
plt.title('residuals, zoom', **title_kwargs)
plt.ylabel(dveff_signed_lbl)
ax4.yaxis.set_label_position('right')
ax4.yaxis.tick_right()
plt.show()
visualize_model_full(pars_try)
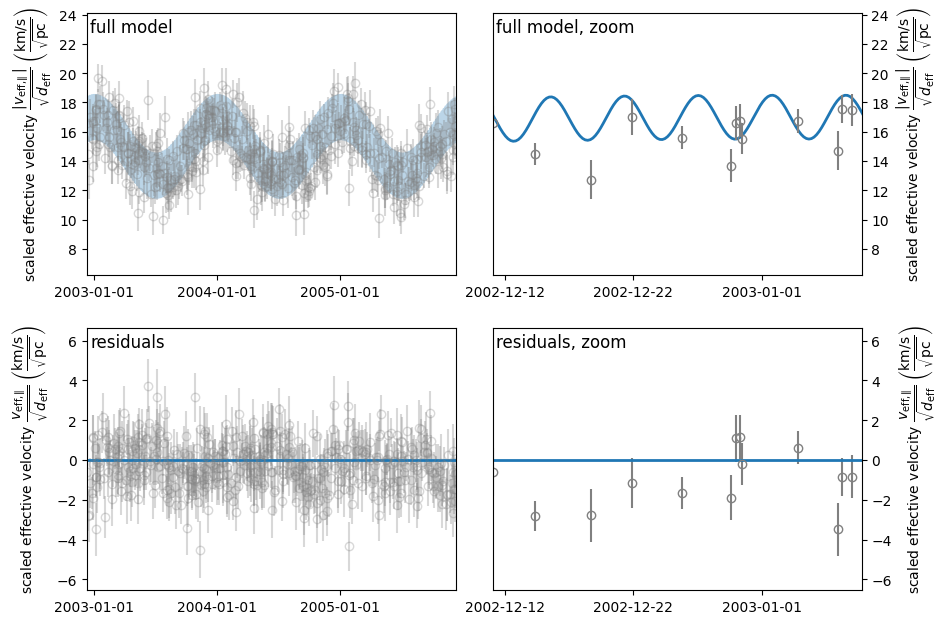
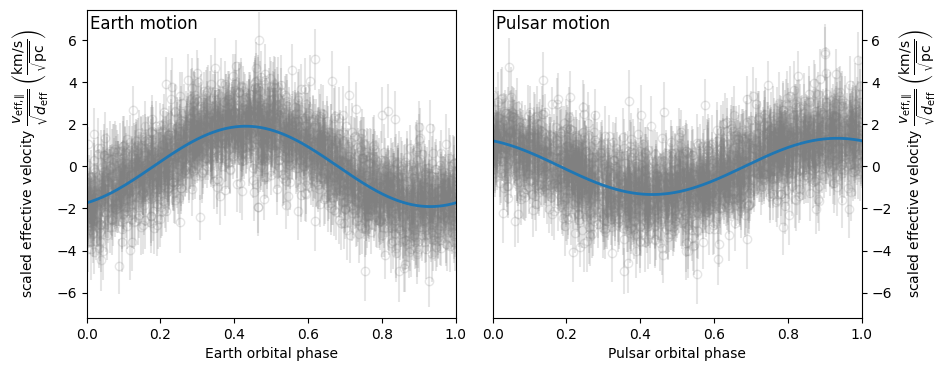
Next, let’s make plots in which the data is folded over the Earth’s and the
pulsar’s orbital period. To do this, it is necessary to generate the
scaled-effective-velocity terms due to Earth’s orbit and the pulsar’s orbit
separately. This can be achieved using the model_dveff_signed() function
(which does not include the modulus operation) and with the parameters of the
other components set to zero. (When copying a dictionary of parameters, pay
attention not to modify the original dictionary.) A model of only the Earth’s
component can then be compared with the data minus the remaining model
components, and likewise for the pulsar. For these plots to show a good
agreement between data and model, all model components need to be accurate,
not just the ones being displayed.
function definition
def visualize_model_folded(pars):
dveff_mdl_full = model_dveff_abs(pars, t_obs)
pars_earth = pars.copy()
pars_earth['amp_p'] = 0. * u.km/u.s/u.pc**0.5
pars_earth['dveff_c'] = 0. * u.km/u.s/u.pc**0.5
dveff_mdl_earth = model_dveff_signed(pars_earth, t_obs)
pars_psr = pars.copy()
pars_psr['amp_e'] = 0. * u.km/u.s/u.pc**0.5
pars_psr['dveff_c'] = 0. * u.km/u.s/u.pc**0.5
dveff_mdl_psr = model_dveff_signed(pars_psr, t_obs)
dveff_res_earth = dveff_obs - dveff_mdl_full + dveff_mdl_earth
dveff_res_psr = dveff_obs - dveff_mdl_full + dveff_mdl_psr
plt.figure(figsize=(10., 4.))
plt.subplots_adjust(wspace=0.1)
ax1 = plt.subplot(121)
idx_e = np.argsort(ph_e_obs.value % 1.)
plt.plot(ph_e_obs[idx_e].value % 1., dveff_mdl_earth[idx_e], **mdl_style)
plt.errorbar(ph_e_obs.value % 1., dveff_res_earth, yerr=dveff_err,
**obs_style, alpha=0.2, zorder=-3)
plt.xlim(0., 1.)
plt.title('Earth motion', **title_kwargs)
plt.xlabel('Earth orbital phase')
plt.ylabel(dveff_signed_lbl)
ax2 = plt.subplot(122, sharey=ax1)
idx_p = np.argsort(ph_p_obs.value % 1.)
plt.plot(ph_p_obs[idx_p].value % 1., dveff_mdl_psr[idx_p], **mdl_style)
plt.errorbar(ph_p_obs.value % 1., dveff_res_psr, yerr=dveff_err,
**obs_style, alpha=0.2, zorder=-3)
plt.xlim(0., 1.)
plt.title('Pulsar motion', **title_kwargs)
plt.xlabel('Pulsar orbital phase')
plt.ylabel(dveff_signed_lbl)
ax2.yaxis.set_label_position('right')
ax2.yaxis.tick_right()
plt.show()
visualize_model_folded(pars_try)
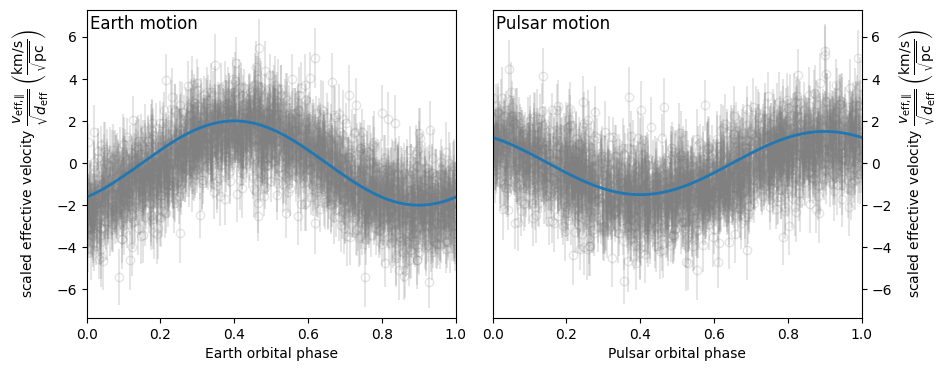
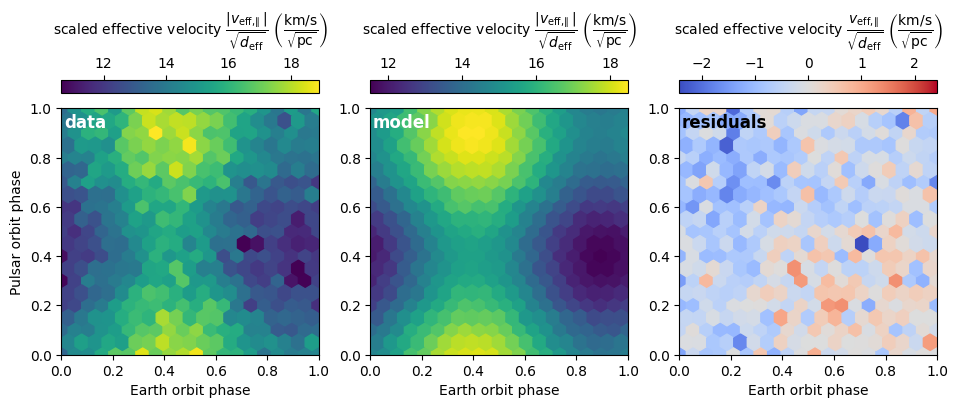
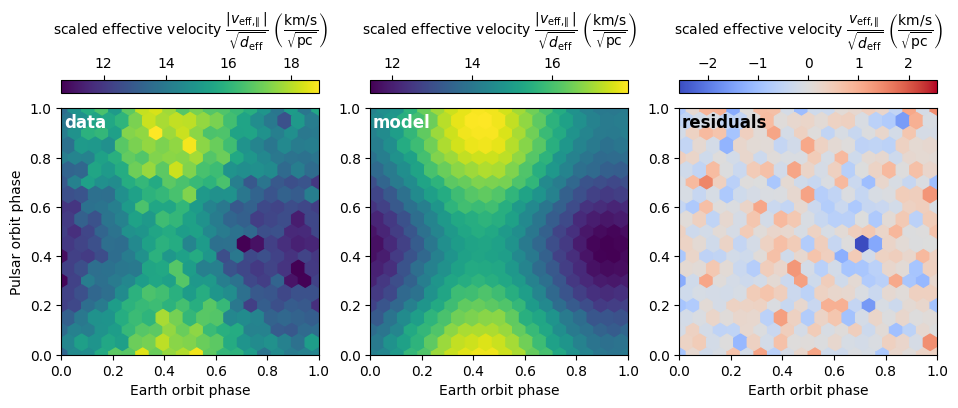
Finally, the 2D phase fold of the data can be compared with the same 2D phase fold of the full model.
function definition
def visualize_model_fold2d(pars):
dveff_mdl = model_dveff_abs(pars, t_obs)
dveff_res = dveff_obs - dveff_mdl
plt.figure(figsize=(11.3, 4.))
gridsize = 19
labelpad = 16
plt.subplot(131)
plt.hexbin(ph_e_obs.value % 1., ph_p_obs.value % 1., C=dveff_obs.value,
reduce_C_function=np.median, gridsize=gridsize)
plt.xlim(0., 1.)
plt.ylim(0., 1.)
plt.xlabel('Earth orbit phase')
plt.ylabel('Pulsar orbit phase')
plt.title('data', **title_kwargs,
fontdict={'color': 'w', 'fontweight': 'bold'})
cbar = plt.colorbar(location='top')
cbar.set_label(dveff_lbl, labelpad=labelpad)
plt.subplot(132)
plt.hexbin(ph_e_obs.value % 1., ph_p_obs.value % 1., C=dveff_mdl.value,
reduce_C_function=np.median, gridsize=gridsize)
plt.xlim(0., 1.)
plt.ylim(0., 1.)
plt.xlabel('Earth orbit phase')
plt.title('model', **title_kwargs,
fontdict={'color': 'w', 'fontweight': 'bold'})
cbar = plt.colorbar(location='top')
cbar.set_label(dveff_lbl, labelpad=labelpad)
plt.subplot(133)
plt.hexbin(ph_e_obs.value % 1., ph_p_obs.value % 1., C=dveff_res.value,
reduce_C_function=np.median, gridsize=gridsize,
norm=CenteredNorm(), cmap='coolwarm')
# Note: CenteredNorm requires matplotlib version >= 3.4.0
plt.xlim(0., 1.)
plt.ylim(0., 1.)
plt.xlabel('Earth orbit phase')
plt.title('residuals', **title_kwargs,
fontdict={'color': 'k', 'fontweight': 'bold'})
cbar = plt.colorbar(location='top')
cbar.set_label(dveff_signed_lbl, labelpad=labelpad)
plt.show()
visualize_model_fold2d(pars_try)
Quantifying the goodness of fit¶
To quantify the goodness of fit of a given instance of the model to the data, we will compute its \(\chi^2\) statistic.
def get_chi2(pars):
dveff_mdl = model_dveff_abs(pars, t_obs)
chi2 = np.sum(((dveff_obs - dveff_mdl) / dveff_err)**2)
return chi2
One can now evaluate the model for a given set of parameter values and compute the corresponding goodness of fit. It may also be useful to calculate the reduced \(\chi^2\) statistic.
chi2 = get_chi2(pars_try)
print(f'chi2 {chi2:8.2f}')
ndof = len(t_obs) - len(pars_try)
chi2_red = chi2 / ndof
print(f'chi2_red {chi2_red:8.2f}')
chi2 3174.65
chi2_red 1.20
Algorithmic maximum likelihood estimation¶
While the above results already look quite good, fitting by eye obviously has
its limitations. To improve on this result, we will now use an optimization
algorithm to find the parameter values that give the maximum likelihood.
Specifically, we will perform a non-linear least-squares fit using the
Levenberg-Marquardt algorithm
as implemented by the SciPy function scipy.optimize.curve_fit().
Note
For data sets with high absolute effective velocities (i.e., with all data
points far away from zero), one can also ignore the modulus operation in
the model equation (eq. \(\ref{eq_model}\)) and perform a (weighted)
linear least-squares fit, for example using scipy.linalg.lstsq().
While the data in the example given here conform to this criterion and a
linear least-squares fit would be more efficient, the non-linear method
presented in this tutorial is more generally applicable. It also works on
data sets with effective velocities around zero, such that the modulus
operation cannot be ignored.
An algorithm-friendly model function¶
The model equation (eq. \(\ref{eq_model}\)) has some properties that make it inconvenient for algorithmic fitting:
The amplitudes \(A_\oplus\) and \(A_\mathrm{p}\) are constrained to be non-negative (\(A_\oplus \geq 0\), \(A_\mathrm{p} \geq 0\)), so the optimization algorithm would need to be configured to avoid the disallowed regions of parameter space.
The phase offsets \(\chi_\oplus\) and \(\chi_\mathrm{p}\) are periodic, with a period of \(360^\circ\). This could cause issues for some fitting algorithms, for example, if the step size in one of these parameters is close to their period.
The equation contains some relatively expensive calculations that can be optimized out to speed up the fitting significantly.
To avoid these complications, the model equation can be recast as
where the amplitudes are related to the amplitudes and phase offsets in eq. \(\ref{eq_model}\) according to
These new amplitudes can be both positive and negative. Results of the fitting can be converted back to the amplitudes and phase offsets in eq. \(\ref{eq_model}\) using
where \(\arctantwo(y, x)\) refers to the 2-argument arctangent function. The constant scaled-effective-velocity offset \(C\) remains the same in both formulations.
Let’s start with building two functions that convert between the two sets of
free parameters, \((A_\oplus, \chi_\oplus, A_\mathrm{p}, \chi_\mathrm{p},
C)\) and \((A_\mathrm{\oplus,s}, A_\mathrm{\oplus,c}, A_\mathrm{p,s},
A_\mathrm{p,c}, C)\).
Because curve_fit() requires the free parameters as
(unitless) floats, these conversion functions also need to convert between a
dictionary of Astropy Quantity objects and
a NumPy ndarray.
def pars_mdl2fit(pars_mdl):
amp_e = pars_mdl['amp_e'].to_value(u.km/u.s/u.pc**0.5)
amp_p = pars_mdl['amp_p'].to_value(u.km/u.s/u.pc**0.5)
chi_e = pars_mdl['chi_e'].to_value(u.rad)
chi_p = pars_mdl['chi_p'].to_value(u.rad)
dveff_c = pars_mdl['dveff_c'].to_value(u.km/u.s/u.pc**0.5)
amp_es = amp_e * np.cos(chi_e)
amp_ec = amp_e * np.sin(chi_e)
amp_ps = amp_p * np.cos(chi_p)
amp_pc = amp_p * np.sin(chi_p)
pars_fit = np.array([amp_es, amp_ec, amp_ps, amp_pc, dveff_c])
return pars_fit
def pars_fit2mdl(pars_fit):
amp_es, amp_ec, amp_ps, amp_pc, dveff_c = pars_fit
amp_e = np.sqrt(amp_es**2 + amp_ec**2)
amp_p = np.sqrt(amp_ps**2 + amp_pc**2)
chi_e = np.arctan2(amp_ec, amp_es)
chi_p = np.arctan2(amp_pc, amp_ps)
pars_mdl = {
'amp_e': amp_e * u.km/u.s/u.pc**0.5,
'amp_p': amp_p * u.km/u.s/u.pc**0.5,
'chi_e': (chi_e * u.rad).to(u.deg) % (360.*u.deg),
'chi_p': (chi_p * u.rad).to(u.deg) % (360.*u.deg),
'dveff_c': dveff_c * u.km/u.s/u.pc**0.5,
}
return pars_mdl
Next, to speed up the fitting, we can precompute the independent variables
\(\sin(\phi_\oplus)\), \(\cos(\phi_\oplus)\)
\(\sin(\phi_\mathrm{p})\), and \(\cos(\phi_\mathrm{p})\) for the
observation times. Again, to comply with the requirements of
curve_fit(), we convert these to floats and store them
in a single NumPy ndarray.
sin_cos_ph_obs = np.array([
np.sin(ph_e_obs).value,
np.cos(ph_e_obs).value,
np.sin(ph_p_obs).value,
np.cos(ph_p_obs).value,
])
Now define the fitting function. To comply with the call signature of
curve_fit(), its first argument should be
the array of independent variables and the following arguments are the fitting
parameters (see below).
def model_dveff_fit(sin_cos_ph, *pars):
amp_es, amp_ec, amp_ps, amp_pc, dveff_c = pars
sin_ph_e = sin_cos_ph[0,:]
cos_ph_e = sin_cos_ph[1,:]
sin_ph_p = sin_cos_ph[2,:]
cos_ph_p = sin_cos_ph[3,:]
dveff_e = amp_es * sin_ph_e - amp_ec * cos_ph_e
dveff_p = amp_ps * sin_ph_p - amp_pc * cos_ph_p
dveff = np.abs(dveff_e + dveff_p + dveff_c)
return dveff
Running the optimizer¶
As a starting point for the fitting, the algorithm needs an initial guess of
the parameter values, ideally already close to the final solution. We can use
the set of parameter values found earlier, pars_try, converted to the
fitting parameters, and cast in the unitless array format expected by
curve_fit().
init_guess = pars_mdl2fit(pars_try)
par_names = ['amp_es', 'amp_ec', 'amp_ps', 'amp_pc', 'dveff_c']
for (par_name, par_value) in zip(par_names, init_guess):
print(f'{par_name:8s} {par_value:8.2f}')
amp_es 1.18
amp_ec 1.62
amp_ps -0.88
amp_pc -1.21
dveff_c 15.00
Everything is now ready to run curve_fit(). It may be
useful to review its call signature:
The first argument is the function to be optimized. Its first argument in turn needs to be the array of independent variables and its remaining arguments are the parameters to adjust.
The second argument is the array of independent variables.
The thrird argument contains the observed data to be fit.
The
p0argument is an array of parameter values that serve as an initial guess.The
sigmaargument is a array of uncertainties on the observed data.
The return values are popt, the optimal parameters found by the algorithm,
and pcov, the covariance matrix of the solution.
popt, pcov = curve_fit(model_dveff_fit, sin_cos_ph_obs, dveff_obs.value,
p0=init_guess, sigma=dveff_err.value)
Checking the result¶
Let’s see what solution the algorithm found.
par_names = ['amp_es', 'amp_ec', 'amp_ps', 'amp_pc', 'dveff_c']
for (par_name, par_value) in zip(par_names, popt):
print(f'{par_name:8s} {par_value:8.2f}')
amp_es 0.80
amp_ec 1.73
amp_ps -0.55
amp_pc -1.22
dveff_c 14.67
To make the result more meaningful and ready as input for our other model
functions, we’ll convert this array into the appropriate dictionary of Astropy
Quantity objects.
pars_opt = pars_fit2mdl(popt)
for par_name in pars_opt:
print(f'{par_name:8s} {pars_opt[par_name]:8.2f}')
amp_e 1.91 km / (pc(1/2) s)
amp_p 1.34 km / (pc(1/2) s)
chi_e 65.14 deg
chi_p 245.83 deg
dveff_c 14.67 km / (pc(1/2) s)
Remember that this is only one of the two solutions. The other solution can easily be computed from the first one and should be identical in data space.
pars_alt = pars_opt.copy()
pars_alt['chi_e'] = (pars_alt['chi_e'] + 180.*u.deg) % (360.*u.deg)
pars_alt['chi_p'] = (pars_alt['chi_p'] + 180.*u.deg) % (360.*u.deg)
pars_alt['dveff_c'] = -1. * pars_alt['dveff_c']
for par_name in pars_alt:
print(f'{par_name:8s} {pars_alt[par_name]:8.2f}')
amp_e 1.91 km / (pc(1/2) s)
amp_p 1.34 km / (pc(1/2) s)
chi_e 245.14 deg
chi_p 65.83 deg
dveff_c -14.67 km / (pc(1/2) s)
How these parameters can be converted to the physical parameters of interest is covered in a follow-up tutorial.
Let’s quantify the goodness of fit of the solution found by the algorithm.
chi2 = get_chi2(pars_opt)
chi2_red = chi2 / ndof
print(f'\nchi2 {chi2:8.2f}'
f'\nchi2_red {chi2_red:8.2f}')
chi2 2598.80
chi2_red 0.98
To check if the fitting worked well, it is also important to visually inspect the solution. This can be done using the visualization functions we made earlier:
visualize_model_full(pars_opt)
visualize_model_folded(pars_opt)
visualize_model_fold2d(pars_opt)
Finally, we use NumPy’s savez() to save the solution and the
accompanying covariance matrix found by curve_fit(),
to do an error analysis in a later tutorial.
np.savez('data/fit-results-J0437.npz',
popt=popt,
pcov=pcov)